2005年05月31日
お~い!竜馬
コンビニで立ち読みをしてしまい、誘惑に勝てずに買ってしまいました。書店で大人買い。最近は古本屋でももうなかなか揃ってないようですね。近所の数軒に電話してみましたがあっても一冊程度。オークションサイトも見てみましたが「今読みたい!」という要求には勝てないものです。買ったのは手に入りやすい文庫版です。

最初に読んだのは連載中だったんでもう何年振りでしょうか。こうやって久しぶりに読むマンガは最初に読んだときとはまた違った趣があります。もちろん自分が変わっているという点において感じ方・感想が変わるという意味です。作品自体は一切変わってないわけですから。こういった感覚は風の谷のナウシカを読み直したときにも感じたなぁ…。
人間の記憶は揮発性メモリみたいなもので、リフレッシュしていなけれ薄れていってしまうようです。ですから一度読んだものでも再度読むことができます。読み直してみるとよく覚えている部分やまったく覚えていない部分が顕著にわかり、これはその当時どの部分に力点をおいて読んでいたかが思い出され非常に楽しい経験であるかと思います。
さて、今後読み返すとしたらなんだろうな。実家の部屋の整理をしたい…。もう何年してないんだか。
2005年05月30日
2005.05.30
ハンドル握れば飲酒量が分かる――飲酒運転を防止する皮膚センサー
http://www.itmedia.co.jp/news/articles/0505/30/news012.html
これ、随分前から考えてたんですがやっぱ他にも同じこと考える人がいますねぇ。私は車と一緒にケータイにも組み込みこんで酔ったときの電話・メールをブロックしたいと考えてました。
NVIDIA、PS3向けのグラフィックスチップはまだ開発中
http://www.itmedia.co.jp/news/articles/0505/28/news009.html
だそうで。
IIJがマザーズ上場へ
http://www.itmedia.co.jp/news/articles/0505/27/news058.html
だそうで。
2005年05月27日
3ヶ月の夢
タイガー!タイガー!もどっタイガー!
復活です。先週の悪評(ただしここだけ)を払拭するような内容でした。まぁこの辺は往往にして好みの問題として存在するものですが。
今、このドラマは7話目ですので中盤も後半にさしかかるくらいです。ドラマというものは、まぁ1クールで完結がほぼ義務付けられているわけで、1つの作品をどんなに楽しみにしていても3ヶ月しか持ちません(ここで連続ものは例外としてはぶきます)。この辺は週刊誌等に代表される連載マンガとは一線を画しているメディアであると捉えることができます。
連載における顧客とドラマにおける顧客の決定的な違いは、それが供給者にとって直接的に利益をもたらす存在であるか間接的に利益をもたらす存在であるか、という点です。この辺は有料チャンネル等を提供する有線放送と現在の地上アナログ放送を比べれば端的だと思われます。
このような状況の中において、どんなに楽しみにしている作品であってもそれが続くのは当初計画された1クールという時間です。かつて、ある人が言いました。「私は小学生低学年の頃、家族と旅行をするのが楽しかった。だが高学年になるにつれて友達とすごす方が楽しくなった。今、自分の子供は小学2年生。彼と一緒に遊べる時間は驚くほどに短い。」
終焉の時期がわかっている好きなドラマに対して視聴者ができることは驚くほどに少ない。ただ応援し、毎週楽しみにして、そして大団円を迎えて、もし許されるなら続編を期待したいものです。ただし、それは先の話。まだまだタイガー&ドラゴンは続きます。
gnuplot(5)
データファイルを使った3次元プロットについて。
# sin_cos_data.plt set xrange [-3:3]; set yrange [-3:3]; set zrange [-2:2] set xlabel "x"; set ylabel "y"; set zlabel "z" set parametric set hidden3d splot "sin_cos.dat" with lines
# sin_cos.dat # x y z -3.000000 -3.000000 0.139708 -3.000000 -2.900000 0.137022 -3.000000 -2.800000 0.132966 -3.000000 -2.700000 0.127583 -3.000000 -2.600000 0.120924 -3.000000 -2.500000 0.113057 -3.000000 -2.400000 0.104061 -3.000000 -2.300000 0.094025 -3.000000 -2.200000 0.083049 : (省略)
sin_cos_data.c
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#define M_RANGE 3
int main(int argc, char *argv[])
{
FILE *fp;
double x, y, z;
fp = fopen( "sin_cos.dat", "w" );
for( x = -M_RANGE; x <= M_RANGE; x += 0.1 )
{
for( y = -M_RANGE; y <= M_RANGE; y += 0.1)
{
z = sin( x ) * cos( y );
fprintf( fp, "%lf %lf %lf\n", x, y, z );
}
fprintf( fp, "\n" );
}
fclose(fp);
return EXIT_SUCCESS;
}
今回は新しいコマンドとして set parametric と set hidden3d があります。
parametric モードは1行に x, y, z の3つの値を持つデータをプロットするモードです。また、ここでは示していませんが noparametric モードは z 値のみを持つ3次元データをプロットするときに使います。
hidden3d は陰線除去を行ってくれるコマンドです。ただ、この設定を行うとグラフの回転表示が非常に遅くなります。どうやら gnuplot はすべてソフトウェアで書かれているようですね。動作環境に応じて OpenGL や Direct3D (非Windows環境では無いので流石にこれは無理だと思いますが)で表示してもらえるといいのですが…。検索してみるとあったりして。
2005年05月26日
2005年05月25日
gnuplot(3)
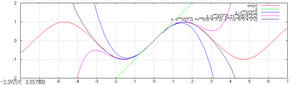
さて、今度はテイラー展開です。
# taylar_sin.plt set xrange [-7:7]; set yrange [-2:2] plot sin(x) replot x replot x -x**3/(3*2) replot x -x**3/(3*2) +x**5/(5*4*3*2) replot x -x**3/(3*2) +x**5/(5*4*3*2) -x**7/(7*6*5*4*3*2)
# taylar_cos.plt set xrange [-7:7]; set yrange [-2:2] plot cos(x) replot 1 replot 1 -x**2/2 replot 1 -x**2/2 +x**4/(4*3*2) replot 1 -x**2/2 +x**4/(4*3*2) -x**6/(6*5*4*3*2)
これらの展開に関しては様々な数学の専門書に書かれていると思いますが、一点あげるならオイラーの贈物をお薦めします。
2005年05月24日
2005.5.24
apple on intel
米アップル、インテル製MPU採用へ・米紙報道
http://it.nikkei.co.jp/it/news/index.cfm?i=2005052402230j0
アップルにチップ乗り換えの可能性
http://japan.cnet.com/news/tech/story/0,2000047674,20083789,00.htm
「憶測に過ぎない」というコメントもあるそうですがかつての歴史(こちらとこちら)を考えると、残すは政治判断のみの状況とうかがえるかもしれません。
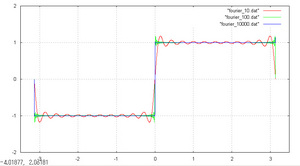
gnuplot(2)
このグラフを表示するためのファイルはこれです。
# fourier_10-10000.plt set xrange [-3.5:3.5]; set yrange [-2:2] plot "fourier_10.dat" with line replot "fourier_100.dat" with line replot "fourier_10000.dat" with line
ここで使用されているファイルは以下にあります。グリッド表示には grid.plt を使います。
これらのデータファイルはpreformatエントリーで示したもので作成されています。というわけでxの範囲は-πからπまでとなります(このフォント、piがすごいですね)。