« 2010年02月 | メイン | 2010年04月 »

CPU 温度 (3)

早速 CPU クーラーを購入して換装してみました。購入したのは以下です。

換装の効果は絶大で、今まで Tj.Max まで行っていた Core 温が 55 ℃近辺まで下がりました。実に -44 ℃です。数値的にだけでなく、精神的にもこれは安心できます。

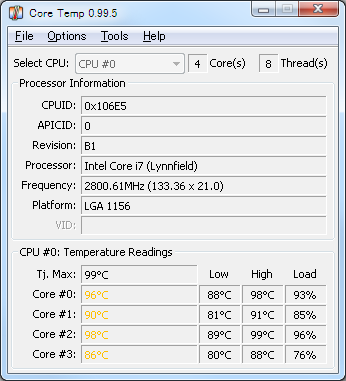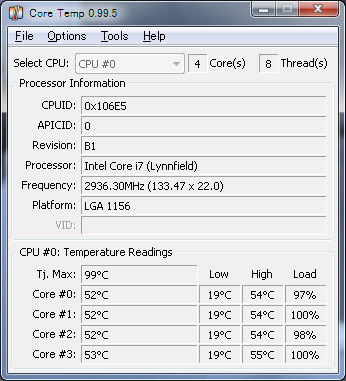CoreTemp.png→CoreTemp2.png
リテールクーラーRR-B10-212P-GP + SG-77001

ただ静音性がだいぶ無い PC になってしまいました（＾＾；ASUS Mother を使っているので Q-Fan の機能を有効にしてみたところかなり静音になりました。この違いは歴然です。 ただやはり、静音性を突き詰めると CONSAIR 製品でまとめたくなりますね、特に電源など。


投稿者 napier : 17:41 | トラックバック


リーマン予想 (2)

本に出てきた名称に関して Wikipedia へのリンクです。個々を調べるための参照用に。若干体系的に理解しやすくなるようにインデントをつけましたが後半はフラットです。特にトポロジー関連と人名はここには入れてありません。

  • 数学 mathematics
  • 数学的構造 mathematical structure
    ブルバキによって全数学を統一的に少数の概念によって記述するために導入された概念。
  • 代数学 algebra
    数の代わりに文字を用いて方程式の解法を研究する学問として始まったが、現代代数学は一般的に代数系を研究する学問分野であると捉えられている。
    • 数論 number theory
      数、特に整数の性質について研究する数学の一分野である。整数論とも言う。ふつうは代数学の一分野とみなされることが多い。
  • 代数的構造 algebraic structure
    集合に定まっている算法（演算ともいう）や作用によって決まる構造のこと。
    • 一つの演算によって決まる代数的構造
      • 群 group
        最も基本的と見なされる代数的構造の一つ。
      • アーベル群 abelian group
        可換群(commutative group)すなわち、定義される乗法が可換な群のこと。
      • 半群 semigroup
        結合法則を満たす二項演算の定義された集合のこと。
      • モノイド
        二項演算の定義された集合の一種である。単系と訳されることもある。
    • 二つの演算によって決まる代数的構造
      • 環 ring
        加法と乗法について閉じている代数的構造を持つ集合。
      • 体 field, Körper, corps
        四則演算の自由にできる代数的構造を備えた集合。
    • その他
  • 集合論 set theory
    集合とよばれる数学的対象をあつかう数学理論。
    • 集合 set
      いくつか（有限または無限）の「もの」からなる「集まり」。慣例的に、ある種の集合が系（けい、system）や族（ぞく、family）などと呼ばれることもある。
      • 元 element; 要素
        複数の「もの」で構成されている集合の中において、集合を構成している個々のものを指す。
      • 系 system
        同時に成立する関係性の組（代数系、方程式系など）。
      • 族 family
        添字付けされた元（要素）の（一般には非可算無限個の）集まりで、対、n-組、列などの概念の一般化。
  • 圏論 category theory
    数学的構造とその間の関係を抽象的に扱う数学理論の 1 つ。考えている種類の「構造」を持った対象とその構造を反映するような対象間の射の集まりからなる圏が基本的な考察の対象になる。
    • 圏 category
      数学的構造とその変形を取り扱うための枠組みであり、数学的対象をあらわす対象とそれらの間の関係を表す射の集まりによってあたえられる。
    • 射 morphism：モルフィズム
      2つの数学的構造の間で構造を保存する過程を抽象化したもの。
    • 関手 functor
      圏論における一つの圏から別の圏への対応でその構造と両立するようなもの。関手は「圏の圏」における射と考えることもできる。
  • 束論 lattice theory
    束 (lattice) に関する理論。
  • 概型 scheme; スキーム
    可換環に対して双対的に構成される局所環付き空間。
  • 代数多様体 algebraic variety
    最も簡略に言えば、多変数の連立多項式系の解集合として定義される図形と述べる事が出来る。
  • 非可換幾何 noncommutative geometry
    可換性が成り立たないような代数構造に対する空間的・幾何学的な解釈を研究する分野。
  • ガロア理論 Galois theory
    代数方程式や体の構造を "ガロア群" と呼ばれる群を用いて記述する代数学の理論。
  • 解析接続 analytic continuation, analytic prolongation
    リーマン球面上の領域で定義された有理型関数に対して定義域の拡張を行う手法の一つ、あるいは、その拡張によって得られた関数の事。
  • 素数定理 Prime number theorem
    自然数の中に素数がどのくらいの「割合」で含まれているかを述べる定理。
  • オイラー積 Euler product
    ディリクレ級数を素数に関する総乗の形で表した無限積。
  • ディリクレ級数 Dirichlet series
    リンク参照。
  • L関数 L-function
    リーマンのゼータ関数を一般化したもの。
  • ガウス整数 Gaussian integer
    実部と虚部が共に整数であるような複素数、すなわち a, b を整数として a + bi の形の複素数のこと。
  • 種数 genus
    数学用語で、分野によって似通っているが微妙に異なる意味を持つ。
  • 素イデアル
    環のイデアルで、ある条件を満たすもの。
  • 完備距離空間: 完備; complete
    距離空間 M が完備であるとは、距離空間 M におけるいかなるコーシー列も M 内の点に収束すること。
  • コーシー列 Cauchy sequence
    数列などの列で、十分先のほうで殆ど値が変化しなくなるもの。実数論において最も基本となる重要な概念の一つ。
  • バーゼル問題 Basel problem
    級数の問題の一つで、Pietro Mengoli によって1644年に提起され、レオンハルト・オイラーが1735年に解いたもの。
  • ヴェイユ予想 Weil conjecture
    数学者のアンドレ・ヴェイユが発表した、リーマン予想の類似で非特異代数多様体上の合同ゼータ関数における予想。
  • p進数 p-adic number
    1897 年にクルト・ヘンゼル によって導入された数の体系の一つ。
  • 岩澤理論 Iwasawa theory
    岩澤健吉が円分体の理論の一部として創始した、（無限次元拡大の）ガロア群の、イデアル類群における表現論。
  • 零点 zero
    ある関数 f によって、0 に移される点、すなわち f(z) = 0 を満たす z のこと。

これらの他、本文中には F1 スキームという手法が取り上げられていましたが Wikipedia には無いようです。少し Web で調べてみたら著者の一人である小島さんのブログに言及がありました。

さて、大まかな概要が分かったところで中身の理解をしなくては。。

最後に一点、この本を読んでいて理解しづらかった言葉に「零点」がありました。ちょっと考えて何を言っているのかわかりましたが、数学用語として存在してるんですね。簡単な言葉だと、値域として 0 となる点、と言った意味です。


投稿者 napier : 14:30 | トラックバック


リーマン予想

こちらのブログ「新・加納裕のBLOGです」の無限級数に関するエントリ[1][2][3][4]を読んでいて興味を持ち、ちょうど休みだったこともあって買って読んでみました。無限級数に関しては大学数学のテスト以降は殆ど使っておらず、このゼータ関数に関しても名前を聞いたことがあるかないかくらいの認識でした。

本の内容としては数式はあまり出さず、言葉による説明と必要最小限の数式によってリーマン予想とは何か、現在までにこの予想を解明するためにどのようなアプローチがとられてきたか、が説明されています。その説明自体は難解ではありませんが（詳しい説明はしないので）、その数が多いことと説明されるそれぞれがどのような関係性で繋がっているかを把握しようとすると、突然数学の海の中に放り込まれます。これは言葉だけではなく図を使った説明があるといいですね（難しいとは思いますが）。

そんなわけで wikipedia とにらめっこで言葉だけでも列挙、と思ってたのですがとても短期間では無理そうです。。とりあえずは簡単に基本だけ。

さて、リンク元のエントリの無限級数の話題は NHK スペシャルが元だったようです。これですね。

それで何個かブログをまわって調べてみたところ、この 50 分の番組とは別に BS Hi で 90 分の拡大版もあったようです。

賛否両論と言ったところのようですね。


投稿者 napier : 01:00 | トラックバック


2010年03月21日

CPU 温度 (2)

少し調べてみると CPU の温度と Core の温度、それぞれがあるようです。まず用語の確認から。

  • Thermal Specification
    温度仕様。最大 Thermal Design Power (TDP) での温度の最大値。これはプロセッサ上部のヒートスプレッダの物理的な中心で計測される。モバイル向けなどの統合されたヒートスプレッダを持たないプロセッサでは、この温度仕様はジャンクション温度 (junction temperature (Tj)) とみなされる。最大ジャンクション温度はインテルの Thermal Monitor を有効化することで定義される。Thermal Monitor のオートマチックモードを使えば最大ジャンクション温度に達したかどうかがわかる。
  • TDP
    Thermal Design Power - 熱設計電力。マイクロプロセッサなどの大規模集積回路で設計上想定される最大放熱量のこと。チップに取り付ける冷却装置を設計する際に、どの程度の冷却能力を持たせれば良いかを決定する為に使われる指標。
  • ヒートスプレッダ
    LSI のパッケージにおいて、LSI チップからの発熱を効果的に放散させるために設けられた金属などの構造部材。
  • Junction temperature
    ジャンクション温度。半導体の最高動作温度。詳しくは以下を。
    　パソコンがうるさいと思ったときの「最高動作温度」
    　放熱板、放熱器(ヒートシンク)の放熱設計法
最高温度の種類
T-JunctionCPU 内部のコアの温度
T-Caseコア表面に装着されている金属製プレート（インテグレーテッド・ヒート・スプレッダー）の中央部分の温度
T-SinkCPU とヒートシンクの接触部中央の温度
T-Ambientヒートシンク上の空気温度

ということで前エントリで調べた 72.7 ℃はこの CPU の T-Case : ヒートスプレッダの最高温度になります。また Core Temp の示す Tj.Max 99 ℃ はコアの最高温度となります。

ふむ、キャプチャ画像で High 表示が 99 ℃まで行っているのは、コアの温度が Tj.Max まで達して Thermal Monitor の保護機構が働いたんでしょうね。そこでクロックを下げるなりして最大温度を超えることがなかったと。熱暴走がおきていない理由はこれで分かりました。

Thermal Monitor に関しては以下のサイトで説明が読めます。

また CPU/Core の温度に関する意見交換が価格.com の口コミでも読めます。


投稿者 napier : 14:13 | トラックバック


2010年03月20日

CPU 温度

CoreTemp.png

エンコード環境も安定動作したこともあり何気に CPU の動作温度を計ってみました。使用したソフトは Core Temp です。結果的には「お？」という温度。ですが今までに熱暴走による再起動やソフトの動作不具合等は全くおきていません。

とりあえず Core i7 860 のスペックの確認を。

Thermal Specification:72.7°C って。。

現在リテールの冷却ファンを使っているのですが、別途専用の冷却ファンを買った方がいいのかもしれませんね。


投稿者 napier : 13:19 | トラックバック


2010年03月14日

涼宮ハルヒの消失 (2)

さて、その 2 です。何の気なしに続きます。

前回のエントリは多分飲んでいたときに書いたので読み返すのが怖くて放置していました。で、今酔っているので(禁酒できてないじゃん！)読み返してみると「ははぁ、言いたいことはわかった」と独りごちるものではありました。そしてその 2 です(ネタバレあり)。

砂の女を読んだこともあって、時空改変された世界がそのまま砂の世界に重なります。劇中でキョンは積極的な帰還を望み、果たしてそれは成し遂げられます。しかしそれは積極的に援助をしてくれる仲間がいたからであり、それもむしろハルヒを中心としたパワーバランスの、その均衡ポイントへ戻すための反作用であったのかもしれません。しかし結果的に語られているのは、狂言回しとしてのキョンの独白を通してのみ、という部分において物語は不動のままです。

この逸話が何を物語っているのかという点において、ひとつ覆せない事実があります。それは長門の関与。そしてそれは、キョンの思う彼の中の長門がそうさせた、だけであるのかもしれません。それは何故か。今回の劇を知っているのはキョン自身と、キョンの認識する長門だけ、であるからです。

・・・いや、劇の最後でキョンの言った意味深なキーワード。「ジョン・スミス」という切り札。これをそのハルヒが本当に知っているか知っていないか。これは重要な連続性の仮定でしょうね。もしかしたら、そのキョンは「ジョン・スミス」を知らないハルヒの世界にいるのかもしれない。

多分に知人の解釈が混ざっており、原作を読んでない自分では判然としないのですが、アニメで語られた内容よりもノベルで語られる物量は尋常ではないらしいので(攻殻機動隊を連想)、その部分に関しても興味がわきます。

原作や人の想像を知らない分妄想できた前回の方の解釈がやはり楽しいですね、自分にとって。ハルヒ自身の解釈(彼女自身の一人称としての独白)がなされる前に、やはり原作を読まなくては。


投稿者 napier : 20:53 | トラックバック


砂の女

第四間氷期に引き続き、阿部公房です。

  • 己のやりたいことを出来ているうちはいいが、知らず知らず望まないことを外圧により強制される。真綿の圧力もあれば理不尽の強制もある。
  • その圧力に比例する形での反発もあれば、その力に絡め取られてしまうこともある。
  • 砂は風の力によってその形を変え、実体としての個は1/8m.m.としてそこにあるが総体としての永続はそこに存在しない。変化することがその存在そのものと言える。
  • 視点/立場を変えると、仏教の色砂で描く砂曼荼羅の修行に通じるかもしれない (完成した曼荼羅はその瞬間に砂へと戻される)。

1 回目に読んでみたときには特に感想がなく、普通の小説だなぁという風にしか思いませんでした。上記は 2 回目の読後感です。これもまた、他の作品を読んだ後に思いかえすためのリファレンスとして。


投稿者 napier : 01:09 | トラックバック


2010年03月12日

不毛地帯

今期、後半からですがちゃんと見ていたドラマです。 2009Q4 から開始しており、全 20 話構成です。久しぶりに見ましたがやはり唐沢さんは安定してますね。和久井映見さんと唐沢寿明といったらかつてのドラマでは鉄板でした。それが今にいたってもの鉄板振りには舌を巻きます。

にもかかわらず、前半 10 話分しっかり録画を忘れてしまっていて、未見のダイジェストのみ。。少し時間が空いたら速攻全話みなくては！です。


投稿者 napier : 23:49 | トラックバック


Previous Page Next Page, All Pages